发表更新项目实践20 分钟读完 (大约3007个字)0次访问

C语言实现五子棋游戏(AI算法实现)

接上文C语言实现五子棋游戏，此文为AI算法的实现

主要为极大极小值搜索中应用Alpha-Beta剪枝

AI 算法

算法思想

AI算法主要思想是，电脑模拟人机双方下棋，并对落子后的局面进行评分，将分值构建成一棵树，再遍历寻找出最优解。

评估函数

  • 首先要先实现对整个棋盘局面打分的评估函数，我设计了一个六元数组来识别五子棋的各种棋形，包括连五，活四，冲四等

  • 然后设计一个各种棋形的权重表，用于打分，赋分有以下几个要点，

    1.对于AI下棋的白棋方来说，将数值赋为正，黑棋棋形赋为负，并且相同棋形下黑棋的权重要更大，应为当AI白棋落子后即为黑子落子。

    2.对于黑棋方(玩家)的连五，活四，冲四，活三等接近胜利的棋形权重要更大，同样原因是AI下完棋就到玩家下棋

    3.棋形分值等级：连5>活4>冲4=活3>眠3=活2>眠2=活1，相邻等级的权重设置为相差20倍（也可以30，40倍），这是因为会重复计算等级比较低的棋型，以此避免影响总体判断。

设计各棋形的分值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//棋子代号
#define C_NONE 0
#define C_BLACK 1
#define C_WHITE 2

//棋型代号 下标 权重
#define OTHER 0//0,其他棋型不考虑
#define WIN 1//100000,白赢
#define LOSE 2//-10000000,黑赢
#define FLEX4 3//50000,白活
#define flex4 4//-80000,黑活
#define BLOCK4 5//400
#define block4 6//-80000
#define FLEX3 7//400
#define flex3 8//-8000
#define BLOCK3 9//20
#define block3 10//-40
#define FLEX2 11//20
#define flex2 12//-40
#define BLOCK2 13//1
#define block2 14//-2
#define FLEX1 15//1
#define flex1 16//-2

初始化棋形判别六元组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
void init_tuple6type() {
    memset(tuple6type, 0, sizeof(tuple6type));
    //白连5,ai赢
    tuple6type[2][2][2][2][2][2] = WIN;
    tuple6type[2][2][2][2][2][0] = WIN;
    tuple6type[0][2][2][2][2][2] = WIN;
    tuple6type[2][2][2][2][2][1] = WIN;
    tuple6type[1][2][2][2][2][2] = WIN;
    tuple6type[3][2][2][2][2][2] = WIN;
    tuple6type[2][2][2][2][2][3] = WIN;
    //黑连5,ai输
    tuple6type[1][1][1][1][1][1] = LOSE;
    tuple6type[1][1][1][1][1][0] = LOSE;
    tuple6type[0][1][1][1][1][1] = LOSE;
    tuple6type[1][1][1][1][1][2] = LOSE;
    tuple6type[2][1][1][1][1][1] = LOSE;
    tuple6type[3][1][1][1][1][1] = LOSE;
    tuple6type[1][1][1][1][1][3] = LOSE;
    //白活4
    tuple6type[0][2][2][2][2][0] = FLEX4;
    //黑活4
    tuple6type[0][1][1][1][1][0] = flex4;
    //白活3
    tuple6type[0][2][2][2][0][0] = FLEX3;
    tuple6type[0][0][2][2][2][0] = FLEX3;
    tuple6type[0][2][0][2][2][0] = FLEX3;
    tuple6type[0][2][2][0][2][0] = FLEX3;
    //黑活3
    tuple6type[0][1][1][1][0][0] = flex3;
    tuple6type[0][0][1][1][1][0] = flex3;
    tuple6type[0][1][0][1][1][0] = flex3;
    tuple6type[0][1][1][0][1][0] = flex3;
    //白活2
    tuple6type[0][2][2][0][0][0] = FLEX2;
    tuple6type[0][2][0][2][0][0] = FLEX2;
    tuple6type[0][2][0][0][2][0] = FLEX2;
    tuple6type[0][0][2][2][0][0] = FLEX2;
    tuple6type[0][0][2][0][2][0] = FLEX2;
    tuple6type[0][0][0][2][2][0] = FLEX2;
    //黑活2
    tuple6type[0][1][1][0][0][0] = flex2;
    tuple6type[0][1][0][1][0][0] = flex2;
    tuple6type[0][1][0][0][1][0] = flex2;
    tuple6type[0][0][1][1][0][0] = flex2;
    tuple6type[0][0][1][0][1][0] = flex2;
    tuple6type[0][0][0][1][1][0] = flex2;
    //白活1
    tuple6type[0][2][0][0][0][0] = FLEX1;
    tuple6type[0][0][2][0][0][0] = FLEX1;
    tuple6type[0][0][0][2][0][0] = FLEX1;
    tuple6type[0][0][0][0][2][0] = FLEX1;
    //黑活1
    tuple6type[0][1][0][0][0][0] = flex1;
    tuple6type[0][0][1][0][0][0] = flex1;
    tuple6type[0][0][0][1][0][0] = flex1;
    tuple6type[0][0][0][0][1][0] = flex1;
 
    int p1, p2, p3, p4, p5, p6, x, y, ix, iy;//x:左5中黑个数,y:左5中白个数; ix:右5中黑个数,iy:右5中白个数
    for (p1 = 0; p1 < 4; ++p1) {
        for (p2 = 0; p2 < 3; ++p2) {
            for (p3 = 0; p3 < 3; ++p3) {
                for (p4 = 0; p4 < 3; ++p4) {
                    for (p5 = 0; p5 < 3; ++p5) {
                        for (p6 = 0; p6 < 4; ++p6) {
                            x = y = ix = iy = 0;
 
                            if (p1 == 1)x++;
                            else if (p1 == 2)y++;
 
                            if (p2 == 1) { x++; ix++; }
                            else if (p2 == 2) { y++; iy++; }
 
                            if (p3 == 1) { x++; ix++; }
                            else if (p3 == 2) { y++; iy++; }
 
                            if (p4 == 1) { x++; ix++; }
                            else if (p4 == 2) { y++; iy++; }
 
                            if (p5 == 1) { x++; ix++; }
                            else if (p5 == 2) { y++; iy++; }
 
                            if (p6 == 1)ix++;
                            else if (p6 == 2)iy++;
 
                            if (p1 == 3 || p6 == 3) {//有边界
                                if (p1 == 3 && p6 != 3) {//左边界
                                    //白冲4
                                    if (ix == 0 && iy == 4) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK4;
                                    }
                                    //黑冲4
                                    if (ix == 4 && iy == 0) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = block4;
                                    }
                                    //白眠3
                                    if (ix == 0 && iy == 3) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK3;
                                    }
                                    //黑眠3
                                    if (ix == 3 && iy == 0) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = block3;
                                    }
                                    //白眠2
                                    if (ix == 0 && iy == 2) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK2;
                                    }
                                    //黑眠2
                                    if (ix == 2 && iy == 0) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = block2;
                                    }
                                }
                                else if (p6 == 3 && p1 != 3) {//右边界
                                   //白冲4
                                    if (x == 0 && y == 4) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK4;
                                    }
                                    //黑冲4
                                    if (x == 4 && y == 0) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = block4;
                                    }
                                    //黑眠3
                                    if (x == 3 && y == 0) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK3;
                                    }
                                    //白眠3
                                    if (x == 0 && y == 3) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = block3;
                                    }
                                    //黑眠2
                                    if (x == 2 && y == 0) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK2;
                                    }
                                    //白眠2
                                    if (x == 0 && y == 2) {
                                        if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                            tuple6type[p1][p2][p3][p4][p5][p6] = block2;
                                    }
                                }
                            }
                            else {//无边界
                               //白冲4
                                if ((x == 0 && y == 4) || (ix == 0 && iy == 4)) {
                                    if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                        tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK4;
                                }
                                //黑冲4
                                if ((x == 4 && y == 0) || (ix == 4 && iy == 0)) {
                                    if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                        tuple6type[p1][p2][p3][p4][p5][p6] = block4;
                                }
                                //白眠3
                                if ((x == 0 && y == 3) || (ix == 0 && iy == 3)) {
                                    if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                        tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK3;
                                }
                                //黑眠3
                                if ((x == 3 && y == 0) || (ix == 3 && iy == 0)) {
                                    if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                        tuple6type[p1][p2][p3][p4][p5][p6] = block3;
                                }
                                //白眠2
                                if ((x == 0 && y == 2) || (ix == 0 && iy == 2)) {
                                    if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                        tuple6type[p1][p2][p3][p4][p5][p6] = BLOCK2;
                                }
                                //黑眠2
                                if ((x == 2 && y == 0) || (ix == 2 && iy == 0)) {
                                    if (tuple6type[p1][p2][p3][p4][p5][p6] == 0)
                                        tuple6type[p1][p2][p3][p4][p5][p6] = block2;
                                }
                            }
                        }
                    }
                }
            }
        }
    }
}

基于以上的棋形分值和判别数组实现对当前棋盘的分值评估

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
EVALUATION evaluate(int(*board)[15]) {
    
    int weight[17] = { 0,1000000,-10000000,50000,-100000,400,-100000,400,-8000,20,-50,20,-50,1,-3,1,-3 };//各棋型权重
    int type;
    int stat[4][17];//统计4个方向上每种棋型的个数
    memset(stat, 0, sizeof(stat));
 
    int STAT[17];//存在这种棋型的方向的个数
    memset(STAT, 0, sizeof(STAT));
 
    int A[17][17];//包括边界的虚拟大棋盘,3表示边界
    for (int i = 0; i < 17; ++i)
        A[i][0] = 3;
    for (int i = 0; i < 17; ++i)
        A[i][16] = 3;
    for (int j = 0; j < 17; ++j)
        A[0][j] = 3;
    for (int j = 0; j < 17; ++j)
        A[16][j] = 3;
    for (int i = 0; i < 15; ++i) {
        for (int j = 0; j < 15; ++j) {
            A[i + 1][j + 1] = board[i][j];
        }
    }
 
    //判断横向棋型
    for (int i = 1; i <= 15; ++i) {
        for (int j = 0; j < 12; ++j) {
            type = tuple6type[A[i][j]][A[i][j + 1]][A[i][j + 2]][A[i][j + 3]][A[i][j + 4]][A[i][j + 5]];
            stat[0][type]++;
        }
    }
 
    //判断竖向棋型
    for (int j = 1; j <= 15; ++j) {
        for (int i = 0; i < 12; ++i) {
            type = tuple6type[A[i][j]][A[i + 1][j]][A[i + 2][j]][A[i + 3][j]][A[i + 4][j]][A[i + 5][j]];
            stat[1][type]++;
        }
    }
    //判断左上至右下棋型
    for (int i = 0; i < 12; ++i) {
        for (int j = 0; j < 12; ++j) {
            type = tuple6type[A[i][j]][A[i + 1][j + 1]][A[i + 2][j + 2]][A[i + 3][j + 3]][A[i + 4][j + 4]][A[i + 5][j + 5]];
            stat[2][type]++;
        }
    }
    //判断右上至左下棋型
    for (int i = 0; i < 12; ++i) {
        for (int j = 5; j < 17; ++j) {
            type = tuple6type[A[i][j]][A[i + 1][j - 1]][A[i + 2][j - 2]][A[i + 3][j - 3]][A[i + 4][j - 4]][A[i + 5][j - 5]];
            stat[3][type]++;
        }
    }
    
    EVALUATION eval;//评估结果
    memset(eval.STAT, 0, sizeof(eval.STAT));
 
    int score = 0;
    for (int i = 1; i < 17; ++i) {
        score += (stat[0][i] + stat[1][i] + stat[2][i] + stat[3][i]) * weight[i];//计分
        int count = stat[0][i] + stat[1][i] + stat[2][i] + stat[3][i];//统计所有方向上部分棋型的个数
        if (i == WIN)
            eval.STAT[WIN] = count;
        else if (i == LOSE)
            eval.STAT[LOSE] = count;
 
    }
    eval.result = R_DRAW;
 
    //白赢
    if (eval.STAT[WIN] > 0)eval.result = R_WHITE;
    //黑赢
    else if (eval.STAT[LOSE] > 0)eval.result = R_BLACK;
 
    eval.score = score;
    return eval;
}

极大极小值搜索

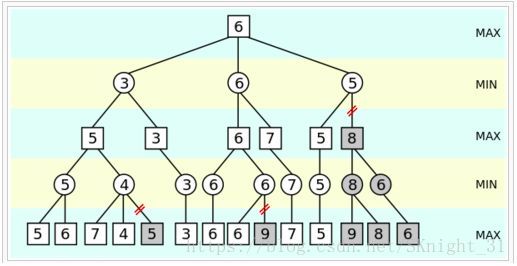
算法的核心环节为极大极小值搜索，首先要引入博弈树的概念，就是将己方和敌方的决策构成树，每个节点的分支表示可走位置，每个叶节点表示一个局面。从根节点为0开始，奇数层表示电脑可能的走法，偶数层表示玩家可能的走法。假设电脑先手，那么第一层就是电脑的所有可能的走法，第二层就是玩家的所有可能走法，以此类推。电脑走棋的层我们称为 MAX层，这一层电脑要保证自己利益最大化，那么就需要选分最高的节点。玩家走棋的层我们称为MIN层，这一层玩家要保证自己的利益最大化，那么就会选分最低的节点。而每一个节点的分数，都是由子节点决定的，因此我们要对博弈树进行深度优先搜索，得到根节点的最佳选择。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
int analyse(int(*board)[15], int depth, int alpha, int beta) {
    gameResult RESULT = evaluate(board).result;
    if (depth == 0 || RESULT != R_DRAW) {//如果模拟落子可以分出输赢，直接返回结果
        if (depth == 0) { //搜索到最后一层
            SOMEPOINTS P;
            P = seekPoints(board); //局部搜索与静态评价启发，直接寻找最佳的可能落子位置
            return P.score[0];  //返回最佳位置对应的最高分
        }
        else {
            return evaluate(board).score; //返回当前层分值
        }
    }
    else if (depth % 2 == 0) {//max层,AI方(白)决策
 
        int sameBoard[15][15];
        copyBoard(board, sameBoard);
        SOMEPOINTS P = seekPoints(sameBoard);
 
        for (int i = 0; i < 10; ++i) {
            sameBoard[P.pos[i].x][P.pos[i].y] = C_WHITE;//模拟AI方落子
            int a = analyse(sameBoard, depth - 1, alpha, beta);//递归搜索
            sameBoard[P.pos[i].x][P.pos[i].y] = C_NONE;//还原落子
            if (a > alpha) {
                alpha = a;
                if (depth == 4) {//搜索深度
 
                    decision.best.x = P.pos[i].x; //AI决策位置
                    decision.best.y = P.pos[i].y;
                    decision.eval = a;
                }
            }
            if (beta <= alpha)break;         //Alpha-Beta剪枝
        }
        return alpha;
    }
    else {//min层,玩家方(黑)决策
 
        int rBoard[15][15];
        reverseBoard(board, rBoard);
        SOMEPOINTS P = seekPoints(rBoard); //寻找黑子的最佳位置，需要反转棋盘颜色
 
        int sameBoard[15][15];
        copyBoard(board, sameBoard);
 
        for (int i = 0; i < 10; ++i) {
 
            sameBoard[P.pos[i].x][P.pos[i].y] = C_BLACK;
            int a = analyse(sameBoard, depth - 1, alpha, beta);
            sameBoard[P.pos[i].x][P.pos[i].y] = C_NONE;
            if (a < beta)beta = a;
            if (beta <= alpha)break;//剪枝
        }
        return beta;
    }
}

Alpha-Beta剪枝

通过遍历博弈树来得到最佳的根节点，即使平均每一步只考虑50个节点，思考深度为四层(才具有一定算力)，搜索的节点数达50^4=6250000个。计算机需要多达100秒才可得到结果，因此我们必须对博弈树剪枝。

α-β剪枝算法应用于此类的极大极小值搜索，思想是在深度优先搜索下，对于提前已经排除选择结果外的节点进行剪枝。

具体实现为每一个节点对应有一个α和一个β，α表示目前该节点的最好下界，β表示目前该节点的最好上界。在最开始时，α为负无穷，β为正无穷。然后进行搜索，max层节点每搜索它的一个子节点，就要更新自己的α（下界），而min层节点每搜索它的一个子节点，就要更新自己的β（上界）。如果更新之后发现α>=β了，说明后面的子节点已经不需要进行搜索了，直接剪枝掉。

进一步优化

局部搜索

对于每次模拟下棋的位置，只需考虑有棋子的附近，无需考虑整个棋盘，能有效减少节点，具体实现为考虑有落子的位置向周围延申三个深度。

静态评价启发

将局部搜索得到的位置，先进行对当前局面的简单评估，只考虑分值较高的前十个节点，并将其排序，并有利于Alpha-Beta剪枝更早地发生。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
SOMEPOINTS seekPoints(int(*board)[15]) {
    bool B[15][15];//局部搜索,每个非空点附近8个方向延伸3个深度
    int worth[15][15];
    SOMEPOINTS best_points;
 
    memset(B, 0, sizeof(B));
    for (int i = 0; i < 15; ++i) {
        for (int j = 0; j < 15; ++j) {
            if (board[i][j] != C_NONE) {
                for (int k = -3; k <= 3; ++k) {
                    if (i + k >= 0 && i + k < 15) {
                        B[i + k][j] = true;
                        if (j + k >= 0 && j + k < 15)B[i + k][j + k] = true;
                        if (j - k >= 0 && j - k < 15)B[i + k][j - k] = true;
                    }
                    if (j + k >= 0 && j + k < 15)B[i][j + k] = true;
                }
            }
        }
    }
 
    for (int i = 0; i < 15; ++i) {
        for (int j = 0; j < 15; ++j) {
            worth[i][j] = -INT_MAX;
            if (board[i][j] == C_NONE && B[i][j] == true) { //对局部搜索的每个位置评估
                board[i][j] = C_WHITE;
                worth[i][j] = evaluate(board).score;
                board[i][j] = C_NONE;
            }
        }
    }
 
    int w;
    for (int k = 0; k < 10; ++k) { //对分数排序出前十个位置
        w = -INT_MAX;
        for (int i = 0; i < 15; ++i) {
            for (int j = 0; j < 15; ++j) {
                if (worth[i][j] > w) {
                    w = worth[i][j];
                    best_points.pos[k].x = i;
                    best_points.pos[k].y = j;
 
                }
            }
        }
        best_points.score[k] = w;
        worth[best_points.pos[k].x][best_points.pos[k].y] = -INT_MAX;//清除掉上一点,计算下一点的位置和分数
    }
    return best_points;
}

至此，AI算法的实现基本完成，优化的结果能达到每步不到0.3秒得到结果。

写在最后

此项目实现的五子棋游戏仍有很多不足之处，UI设计较为简陋，AI算法仍有很多提高之处。

完成项目的过程中也遇到了很多困难，也参考了许多教程和源代码，在此列出以表感谢。

陈可佳 博弈五子棋

livingsu 基于c++和qt实现五子棋ai

这是此项目的GitHub链接

github.com/Sami-zzz/gobang

#
关注我

最新文章

目录

分类

标签

AI算法2
C++2
CSS1
C语言2
JavaScript5
Typescript1
axios1
vue33
二分2
刷题2
前端9
双指针3
数组2
笔记5
算法4
链表1
项目4

链接

×